Cellular Automata: Introduction

Table of Contents
Introduction
Galaxy formations, solar systems, biological organisms and the intricate assembly of molecules. The universe is full of complexity at every scale. In fact, this complexity is so vast that for part of the population, it serves as a proof [1] of an intelligent designer (i.e. a "god"). The reasoning behind this thinking is, that something incredibly complex and rich must originate from a deeply intricate source. Complexity cannot simply appear out of thin air.. or can it?
While modern variations of Cellular Automata are successfully used in computational Biology, Chemistry, as well as Social Science and other fields, Stephen Wolfram, in his 2002 book 'A New kind of Science' [2], used them to challenge the idea that complexity necessitates a complex source. In this introductory post, I want to explore the most simple type of Cellular Automata (CA). We will see how even from the most simple rules and initial conditions, richness and complexity organically arises.
But What is a Cellular Automaton?
As the name suggests, a CA is an automaton (i.e. a machine following a pre-defined set of rules) acting on a structured set of cells. Each cell has a state, the state of each cell changes over time as a result of the action applied to it. The action is pre-defined and based on:
- the state of the cell itself
- the state of its neighboring cells
This is as deep as the definition of CAs goes. How exactly a rule looks like depends on the definition of the cell and the structure they are arranged in. These structures can get quite intricate, such as in the 'Lenia'[3] CA that is used to simulate Artificial Life.
The simple Wolfram Cellular Automaton
But CAs don't need to be complex. In Wolfram's first experiments, he used the most simple CA possible:
- A cell can be in one of two states:
- State 1 is represented with a white tile
- State 2 is represented with a black tile
- The cells are arranged on a line as in (Fig.1)

Fig.1: Example of a CA consisting of six cells.
Now that the structure of the automaton is defined, we can think about the actions. Recalling the general definition of CAs, an action is based on the state of the cell and its neighboring cells. In the case of the simple Wolfram CA, a cell has exactly two neighbors: one to its' left and one to its' right. Each neighbor can be either in state 1 or in state 2. Additionally, the cell itself can be in either of the two states.
We can define a rule for each of these situations. E.g.: 'If the left neighbor has a black tile, the right neighbor a black tile, and the cell itself a white tile, the cell shall become black at the next step'. (Fig.2) visualizes the rule I have just described.
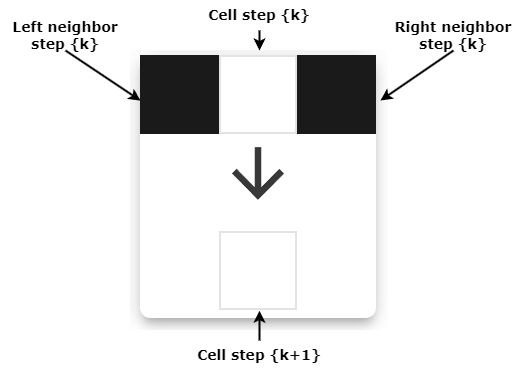
Fig.2: The rule cards of the cellular automaton visualize how to perform updates
A ruleset has a defined rule for each possible situation. A rule can have two outcomes: either the cell becomes black or white at the next step. We know the amount of possible situations (8) and we know the amount of possible outcomes for each situation (2).
Interactive Cellular Automaton
We now understand how the classic Wolfram CA works in theory. What is left is to see it in practice. For this purpose, I have prepared an interactive CA. In order to try it out, you can:
- Define the ruleset by clicking on the 'outcome' cells on the rule cards
- Adjust the size of the grid and the animation speed to your liking
- Define the starting state of the automaton by clicking on the cells
- Run the CA
Discussion
If you tried out the rulesets suggested in the interactive CA, you will have come across patterns like the ones shown in (Fig.3). I hope that I am not alone in thinking, that it is beautiful, what intricate patterns grew out of a single seed cell combined with what is almost the simplest possible ruleset. Wolfram's classic CA experiments are clear evidence that complexity does not necessitate a complex source. Rather, the rules that govern even our universe may be vastly simple.

Fig.3: Examples of the patterns generated by the CA over time using different rulesets.
In future posts, I aim to look at more modern applications of Cellular Automata. I hope that this serves as a nice introduction to the topic and provides a glimpse into the possibilities that more sophisticated CAs can provide.
Credits
[1] Dembski, W.A., 2002. Intelligent Design: The Bridge Between Science Theology. InterVarsity Press.
[2] Wolfram, S., 2002. A new kind of science. Champaign, Ill.: Wolfram Media.
[3] Chan, B.W.C., 2018. Lenia-biology of artificial life. arXiv preprint arXiv:1812.05433.